7장 선형회귀(linear regression)

1. 선형 회귀

선형 회귀 : 실수 벡터 입력이 주어졌을 때 선형적 관계를 지닌 출력 실수 벡터 값을 예측하는 문제

 

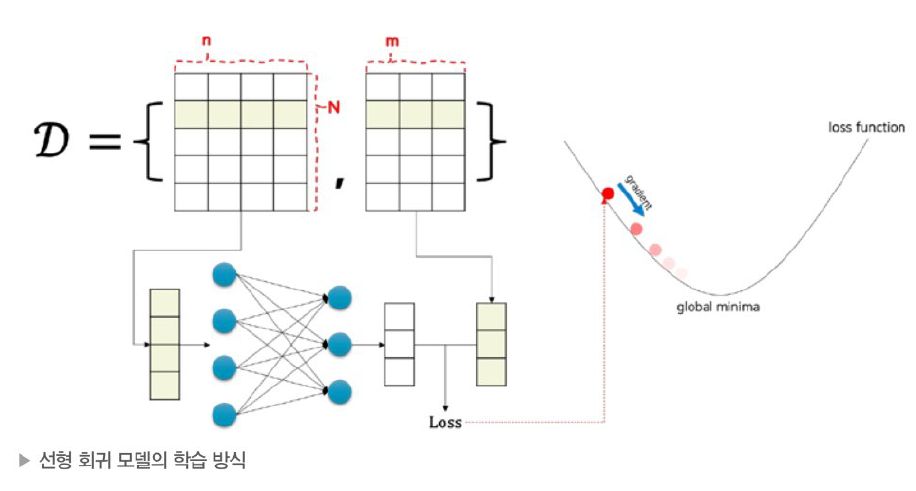
n차원의 입력, m차원의 출력, 데이터 N개 

loss값을 가중치 파라미터로 미분하여 loss 값을 낮추는 방향으로 파라미터 업데이트

-> 손실함수를 최소화하는 가중치 파라미터를 가진 선형 회귀 모델

 

2. 선형 회귀의 수식

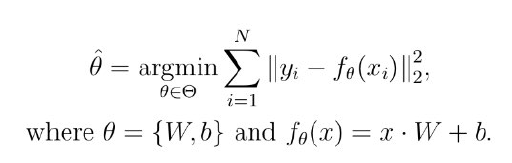
선형회귀의 손실함수는 주로 MSE 손실 함수를 사용

각각의 샘플을 따로 계산하는 대신 행렬로 한꺼번에 계산 가능

 

W와 b로 각각 손실함수를 편미분한 후 경사하강법을 통해 업데이트

 

3. 선형회귀 실습

import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.datasets import load_boston
boston=load_boston()
print(boston.DESCR)

df=pd.DataFrame(boston.data, columns=boston.feature_names)
df["TARGET"]=boston.target
df.tail()

sns.pairplot(df)
plt.show()

cols=["TARGET","INDUS","RM","LSTAT","NOX","DIS"]
sns.pairplot(df[cols])
plt.show()

 

선형관계띄는 일부 속성만 추려내어 pairplot

 

<선형회귀 모델>

import torch
import torch.nn as nn
import torch.nn.functional as f
import torch.optim as optim

data=torch.from_numpy(df[cols].values).float()
y=data[:,:1]
x=data[:,1:]
n_epochs=2000
learning_rate=1e-3
print_interval=100

model=nn.Linear(x.size(-1),y.size(-1))
print(model)
optimizer=optim.SGD(model.parameters(),lr=learning_rate)

for i in range(n_epochs):
    y_hat=model(x)
    loss=f.mse_loss(y_hat,y)
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
    if(i+1)%print_interval==0:
        print('Epoch %d: loss=%.4e'%(i+1,loss))

backward함수+step함수 -> 경사하강 1번 수행

optimizer.zero_grad(): 그래디언트를 0으로 초기화! 초기화하지 않으면 미분한 값들이 누적됨.

 

<결과확인> -> y와 y_hat 비교

df=pd.DataFrame(torch.cat([y,y_hat],dim=1).detach_().numpy(), columns=["y","y_hat"])
sns.pairplot(df,height=5)
plt.show()