8장. 로지스틱 회귀

선형회귀는 연속형 변수를 예측하지만 로지스틱 회귀는 주로 이진분류를 위해 사용됨 (0또는 1)

로지스틱 회귀는 데이터가 어떤 범주에 속할 확률을 0~1 사이 값으로 예측하고,
그 확률에 따라 가능성이 더 높은 범주에 속하는 것으로 분류

 

1. 활성함수

선형계층 함수 직후에 -> 활성함수를 넣어주어 전체 모델 구성

 

대표적인 활성함수: 시그모이드 함수, 탄에이치함수

 

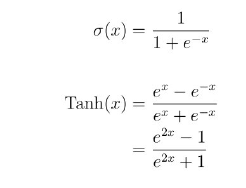
시그모이드 함수: 0~1

탄에이치: -1~1

 

2. 손실함수

 

이진분류문제를 푸는 경우 -> 이진 크로스엔트로피(BCE) 손실함수

 

3. 로지스틱 회귀의 수식

손실함수

 

이때, 확률 값의 표현이라고도 볼 수 있다.

 

4. 실습

import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt

from sklearn.datasets import load_breast_cancer

cancer=load_breast_cancer()

df=pd.DataFrame(cancer.data, columns=cancer.feature_names)
df['class']=cancer.target

cols=['class']+list(df.columns[:10])
sns.pairplot(df[cols])
plt.show()

for c in cols[1:]:
    sns.histplot(df, x=c, hue=cols[0], bins=50, stat='probability')
    plt.show()

 

두 클래스가 구분이 잘 될수록 로지스틱 회귀에 알맞은 속성

 

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim

cols=["mean radius","mean texture","mean smoothness", "mean compactness","mean concave points", "worst radius","worst texture","worst smoothness","worst compactness","worst concave points","class"]

data=torch.from_numpy(df[cols].values).float()

x=data[:,:-1]
y=data[:,-1:]

n_epochs=200000
learning_rate=1e-2
print_interval=10000

class MyModel(nn.Module):
    def __init__(self, input_dim, output_dim):
        self.input_dim=input_dim
        self.output_dim=output_dim

        super().__init__()

        self.linear=nn.Linear(input_dim, output_dim)
        self.act=nn.Sigmoid()

    def forward(self, x):
        y=self.act(self.linear(x))
        return y
        
        
model=MyModel(input_dim=x.size(-1),output_dim=y.size(-1))
crit=nn.BCELoss()
optimizer=optim.SGD(model.parameters(), lr=learning_rate)

for i in range(n_epochs):
    y_hat=model(x)
    loss=crit(y_hat, y)
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

    if(i+1)%print_interval==0:
        print('Epoch %d: loss=%.4e'%(i+1, loss))

loss가 계속 줄어든다!

 

정확도 계산

correct_cnt=(y==(y_hat>.5)).sum()
total_cnt=float(y.size(0))
print("Accuracy: %.4f"%(correct_cnt/total_cnt)) #0.9649

 

df=pd.DataFrame(torch.cat([y,y_hat],dim=1).detach().numpy(), columns=["y","y_hat"])
sns.histplot(df,x='y_hat',hue='y',bins=50, stat='probability')
plt.show()

각 클래스별 분포가 양 극단으로 치우쳐져 있으면 예측 잘한것