하이퍼파라미터: 모델의 성능에 영향을 끼치지만 자동으로 최적화되지 않는 파라미터
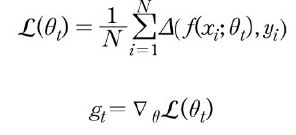


1. 모멘텀
모멘텀은 시작부터 매번 계산된 그래디언트를 누적하는 형태로 구현(관성을 의미)
지역 최소점을 쉽게 탈출할 수 있으며 학습 속도를 가속화할 수 있음


모멘텀 그래디언트: 처음부터 현재까지의 디스카운트 파라미터가 곱해진 그래디언트의 누적 합

하지만 여전히 학습률 튜닝 필요 : 누적된 그래디언트가 파라미터 업데이트에 끼치는 영향도 설정
2. 적응형 학습률
학습률을 기본 설정값을 사용하더라도 학습이 잘되는 방법 필요
- 학습률 스케줄링

학습률이 크면 학습 후반에 더 나은 손실 값을 얻기 히들고,
학습률이 작으면 학습 초반에 너무 더딘 학습을 하게 됨
적응형 학습률: 처음에는 큰 학습률로 가져가되, 현재 에포크의 손실 값이 지난 과거 에포크의 손실 값보다 나아지지 않으면 학습률을 일정 비율(감쇠비율: learning rate decay ratio 보통 0.5 또는 0.1)로 줄이는 방법
-> 동적 학습률
1) 아다그래드 옵티마이저
- 최초로 제안된 적응형 학습률 알고리즘
- 가중치 파라미터마다 별도의 학습률을 가진다
- 각 가중치 파라미터의 학습률은 가중치 파라미터가 업데이트될수록 반비례하여 작아진다.
즉, 학습초반에는 큰 학습률, 학습 후반에는 작은 학습률
- 파라미터 업데이트가 많이 될 경우 학습률이 너무 작아져 나중에는 업데이트가 잘 이루어지지 않음


학습률이 여전히 있기는 하지만, 학습이 진행됨에 따라 점점 영향도가 작아지고, 별다른 튜닝 없이 기본 설정값을 가지고 준수한 성능을 얻어낼 수 있다.
2) 아담 옵티마이저
-기존 적응형 학습률 방식 + 모멘텀
- 가장 보편적으로 쓰이는 알고리즘
- 내부 하이퍼파라미터 갖고 있지만 기본 세팅으로 가도 무방



디스카운트 파라미터 p2가 반복되어 곱해지기 때문에 학습 후반으로 갈수록 그래디언트의 제곱값의 누적이 마냥 커지는 것을 방지



(2): 상수취급
(3): 모멘텀
(4): 적응형 학습률
(1): 편향수정(bias correction)

학습 극초반에 불안정하게 의도치 않은 방향으로 학습이 진행되는 것을 방지
여전히 학습율이 수식에 있지만 대부분 기본값으로 두어도 잘 동작함
3. 실습 (Adam optimizer)
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import fetch_california_housing
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
california=fetch_california_housing()
df=pd.DataFrame(california.data, columns=california.feature_names)
df["Target"]=california.target
scaler=StandardScaler()
scaler.fit(df.values[:,:-1])
df.values[:,:-1]=scaler.transform(df.values[:,:-1])
data=torch.from_numpy(df.values).float()
x=data[:,:-1]
y=data[:,-1:]
print(x.shape, y.shape)
n_epochs=4000
batch_size=256
print_interval=200
model=nn.Sequential(
nn.Linear(x.size(-1),6),
nn.LeakyReLU(),
nn.Linear(6,5),
nn.LeakyReLU(),
nn.Linear(5,4),
nn.LeakyReLU(),
nn.Linear(4,3),
nn.LeakyReLU(),
nn.Linear(3,y.size(-1))
)
optimizer=optim.Adam(model.parameters())
for i in range(n_epochs):
indices=torch.randperm(x.size(0))
x_=torch.index_select(x,dim=0, index=indices)
y_=torch.index_select(y,dim=0, index=indices)
x_=x.split(batch_size, dim=0)
y_=y.split(batch_size, dim=0)
y_hat=[]
total_loss=0
for x_i, y_i in zip(x_, y_):
y_hat_i=model(x_i)
loss=F.mse_loss(y_hat_i, y_i)
optimizer.zero_grad()
loss.backward()
optimizer.step()
total_loss+=float(loss)
y_hat+=[y_hat_i]
total_loss=total_loss/len(x_)
if(i+1)%print_interval==0:
print('Epoch %d: loss=%.4e'%(i+1, total_loss))
y_hat=torch.cat(y_hat, dim=0)
y=torch.cat(y_, dim=0)
df=pd.DataFrame(torch.cat([y,y_hat], dim=1).detach().numpy(), columns=["y","y_hat"]
sns.pairplot(df, height=5)
plt.show()'딥러닝 > 파이토치 딥러닝' 카테고리의 다른 글
| 13장. 심층신경망2 (0) | 2024.05.15 |
|---|---|
| 12장. 오버피팅을 방지하는 방법 (0) | 2024.05.15 |
| 9장. 심층신경망 (0) | 2024.05.02 |
| 8장. 로지스틱 회귀 (1) | 2024.05.01 |
| 7장 선형회귀(linear regression) (0) | 2024.04.22 |



